如何將 AI 應用於金融商品交易領域，一直是個熱門議題。例如預測下一個時間段的漲跌，進而判斷是否要進場？

這篇文章將聚焦於 AI 在金融商品交易領域的應用。我們會介紹一篇名為《Financial Markets Prediction with Deep Learning》（註1）的論文，並附上筆者評論，同時嘗試複現論文中提出的方法，將其應用於台指期貨交易，以驗證其效能。（Demo 程式碼可於文末取得）

該論文提出了一個新穎的模型結構，更在問題定義、預測目標 Y label 的界定方式，以及尋求實際交易場景下可應用的評估指標等方面，做出有意義的貢獻且極具參考價值。不僅有助於深入了解金融市場預測挑戰，也為實際利用 AI 交易策略的制定提供有益的建議，因此，本次我們選擇分享這篇論文，希望能將其中的觀點傳遞給讀者。

定義問題

AI 目前在金融交易上的應用，不外乎為預測漲跌（分類問題）、預測下一時間的價格（迴歸問題），或是使用強化學習讓 AI 模型直接操作買賣，這些皆是希望達到低買高賣、高賣低買等目的，使交易能夠有正損益。

本文主要希望預測下一個時間段是漲、跌或平盤，進而讓交易者能夠判斷是否要進場進行交易。因此，可將此視為分類問題。

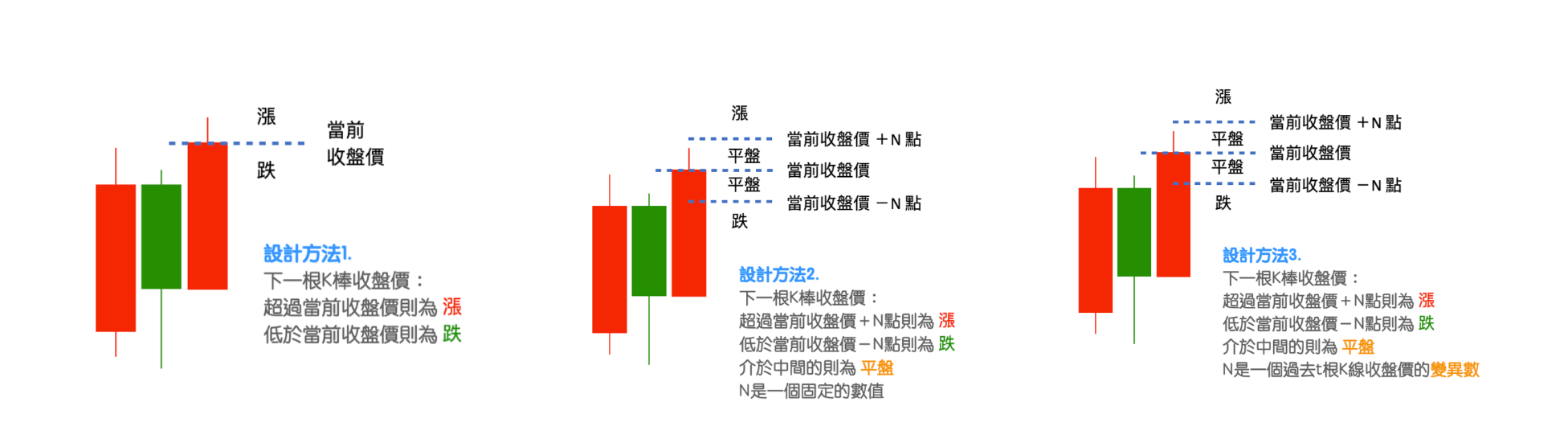
預測目標的設計，這邊有幾種制定方法，舉例說明如下：

1. 根據下一個 K 線收盤價大於或小於當前 K 線收盤價，訂出漲或跌

2. 當目標超過某個範圍，例如下一個 K 線的收盤價漲跌，超過前一個 K 線收盤價 20 點，就稱為漲/跌/平盤

3. 根據前幾筆資料的價格波動來制定範圍，因為下一個 K 線的漲跌幅，往往會根據前一段時間的盤勢而有變化，例如當前盤勢走動很劇烈，那可以想像下一個 K 線會走出一大段的機率很高。這也是這篇論文使用的方法，論文使用當前 K 線往回數 10 個 K 線收盤價的變異數，乘上一個變數後決定這個範圍，公式如下:

   $$l_{t+1} \begin{cases} up, &if\ c_{t+1} \ge c_t(1+\alpha v_t) \\ down, &if \ c_{t+1} \le c_t(1-\alpha v_t)\\ flat, &otherwise \end{cases}$$

   其中 $c_t$ 代表 $t$ 時間點的收盤價，$\alpha$ 是一個常數，論文中設定為 0.55，$v_t$代表一段時間的變異數，這裡是設定 10 個時間的變異數。

   
   （圖片來源：人工智慧科技基金會）

   資料型態

   1. 原始資料：
      1. 包含幾種商品：輕原油期貨（CL）、天然氣期貨（NG）、黃豆期貨（S）、黃金期貨（GC）、那斯達克 100 指數期貨（NQ）、標普 500 期貨（ES）
      2. 2010 年 1 月 - 2017 年 12 月，每個商品含有約 33 萬-40 萬筆 5 分 K 的資料。
      3. 資料欄位有: date, time, open price, high price, low price, close price, trading volume，共六個欄位。
   2. 額外使用的技術指標:
      1. EMA、MACD、Bollinger Bands、RSI、CCI、VWAP、OBV、ADX、ADL、CMF、ROC。
   3. 模型預測的方法為利用歷史的兩個小時的時間段，去預測下一根五分 K 是漲或跌，來輔助交易決策。兩個小時的資料段包含了 24 個 5 分 K 資料，所以這個模型會參考兩小時去預測下一個五分鐘的盤勢如何走，筆者認為也可以拉得更長，有時候則需要參考更前一天的走勢等。

   模型設計

   • Cross-Data-Type One-dimensional Convolution (CDT 1D-CNN)

   

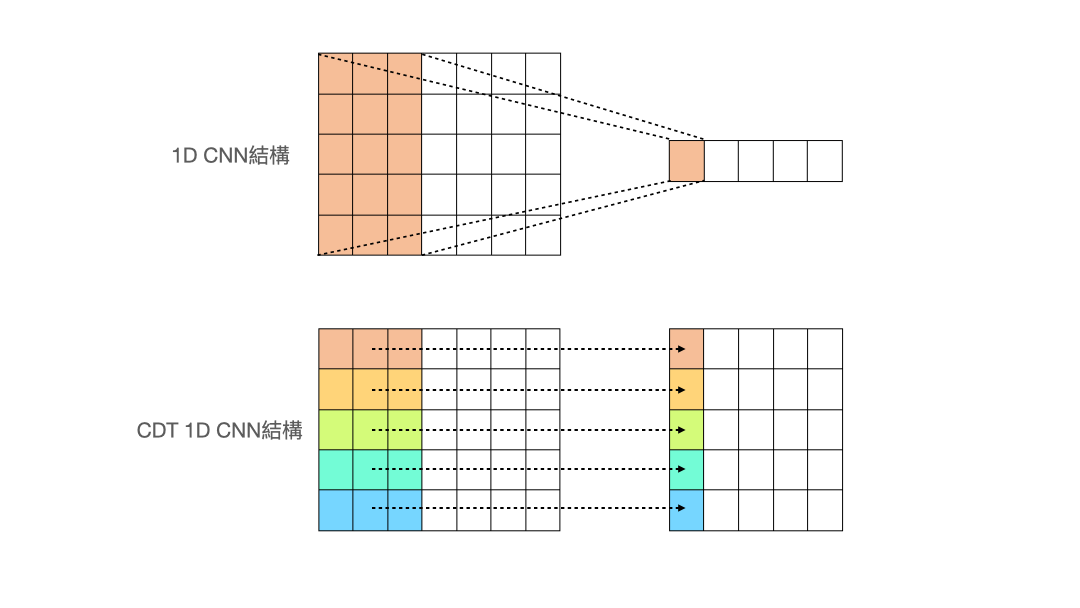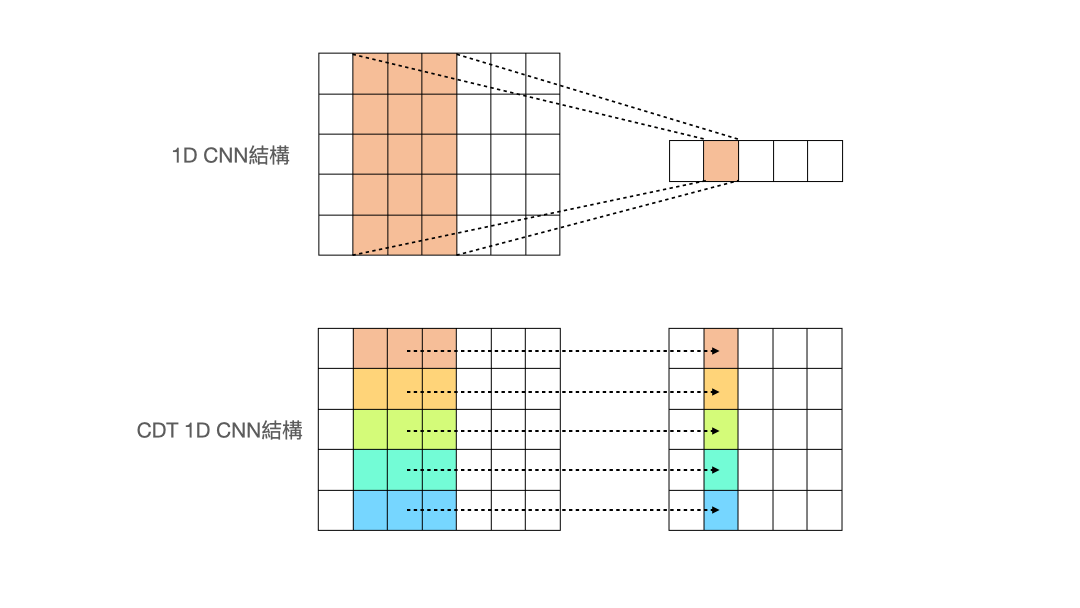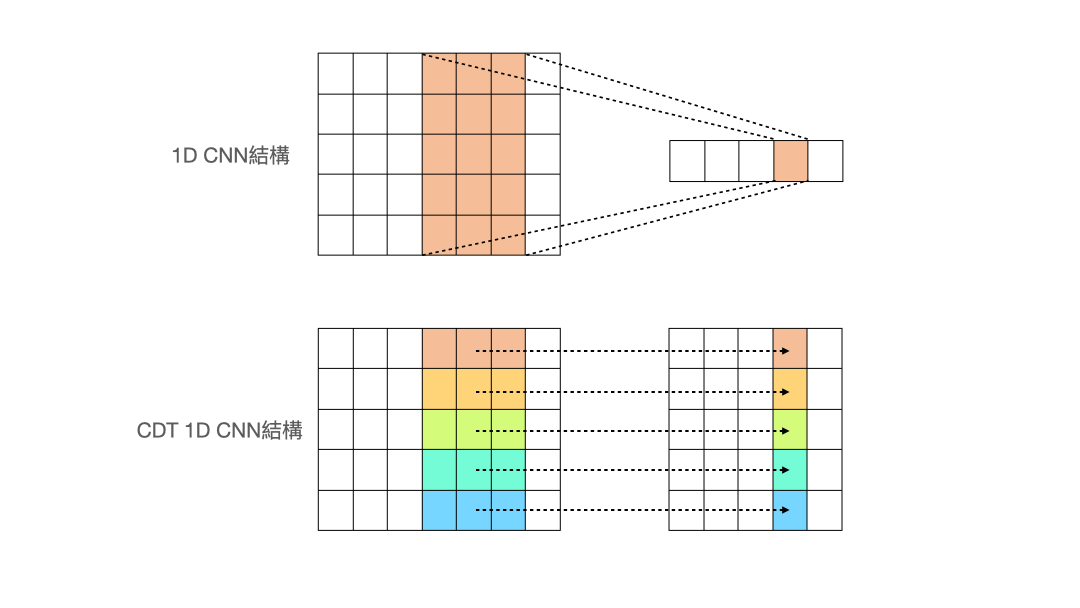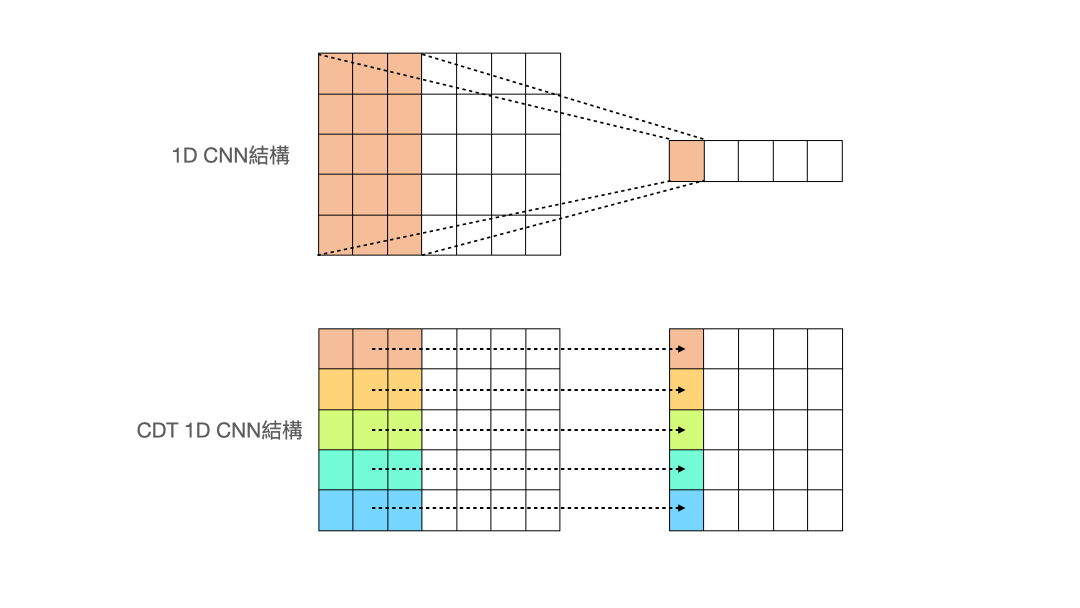
   作者設計了一個名為 Cross-Data-Type One-dimensional Convolution 的 CNN 結構，從上面的動畫可以看出與一般的 1d-CNN 不同，作者希望做卷積的過程，能讓每個特徵獨立去卷積，而不是像一般的 1d-CNN 會把所有特徵同時捲入做計算。

   論文中的結構設計如下：

   

   除了上述的 CDT 1-D CNN 結構之外，可以看到該文作者在 MaxPooling 的作法也是相同概念，在得到所有的特徵圖後，接著才進入全連接層中做特徵的運算。

   筆者自己用類似概念刻的模型參考：

   def SimpleModel(input_shape):
   
       Input = keras.Input(shape=(input_shape), name="input")
           
       # x = tf.transpose(Input, [0,2,1])
       x = tf.expand_dims(Input, -1)
       x = layers.Conv2D(64, (4,1), activation='relu' ,strides=(1,1), padding="same")(x)
       x = layers.Conv2D(64, (4,1), activation='relu' ,strides=(1,1), padding="same")(x)
       x = layers.MaxPool2D((4,1),strides=(4,1))(x)
   
       x = layers.Conv2D(128, (3,1), activation='relu' ,strides=(1,1), padding="same")(x)
       x = layers.Conv2D(128, (3,1), activation='relu' ,strides=(1,1), padding="same")(x)
       x = layers.MaxPool2D((3,1),strides=(3,1))(x)
   
       x = layers.Conv2D(256,(2,1), activation='relu' ,strides=(1,1), padding="same")(x)
       x = layers.Conv2D(256,(2,1), activation='relu' ,strides=(1,1), padding="same")(x)
       x = layers.MaxPool2D((2,1),strides=(2,1))(x)
           
       x = layers.Flatten()(x)
       x = layers.Dense(1000)(x)
       x = layers.Dense(500)(x)
       x = layers.Dense(3, activation="softmax")(x)
       
       return  keras.Model(Input, x, name="MyModel")
   
   Attribute_size, Period =  31, 24
   model = SimpleModel((Period, Attribute_size))
   model.summary()

   筆者認為這樣的設計是符合邏輯的，經過這樣的運算後，下一層 feature map 的每一欄，都還是保持著各個獨立特徵運算後的結果。最後，再經由全連接層運算後，理論上是真的能透過模型自行訓練，並產生出一個新的技術指標。因為每個技術指標背後，也都是由成交價、成交量、時間區間等資訊，經過四則運算計算出來的結果。

   模型評估

   在評估方面，有幾個面向可以考量，其中：

   1. 實際使用這個模型進行交易，期望能夠得到最大的回報，也就是能賺錢
   2. 評估風險，除了賺多少錢之外，也想看使用這個交易策略承擔多少賠錢的風險，也就是夏普值
   3. 在 AI 模型使用上，當然會想看分類的評估指標，在這裡作者提出一個從 F Score 改良的 Weighted F-Score，讓這個評估指標更符合使用。

   以下就分別介紹這三種考量的指標：

   1. 實際交易回測
      • 這篇論文的作者們，設計了一套方法來做歷史資料的交易回測，設定的細節筆者在這就不贅述，可以到原文中閱讀（註2），這邊只放回測的收益結果圖。

   
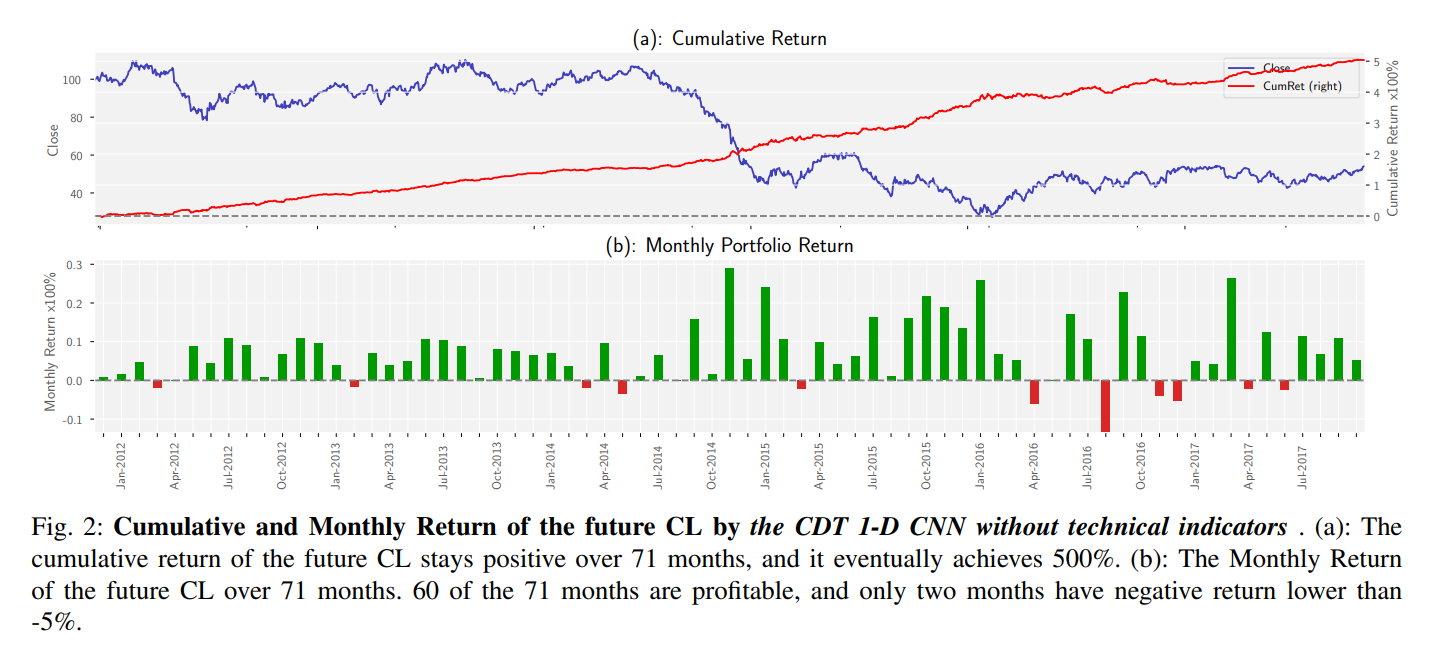
   （圖片來源：註1）

   2. 較高的夏普值（Sharpe ratio）
      • 夏普值不是一個在分類模型中可以立即使用的評估指標，例如準確度、Recall、Precision 都是可以直接影響到模型好壞的指標，甚至直接拿來當成 loss function 來影響模型的學習方向，夏普值則是需要透過回測後才能得到指標，通常做量化交易、程式交易的策略都會評估夏普值，因為除了看收益外，還需要檢視過程中能承受多少的回檔風險，越高的夏普值，代表每賺一個單位，所承受的風險越低。
   3. Weighted F-Score
   $N_{tp}=N_{tu}+N_{td}+\beta^2_3N_{tf}$

   $E_{1st}=E_{wutd}+E_{wdtu}$

   $E_{2nd}=E_{wutf}+E_{wdtf}$

   $E_{3rd}=E_{wftu}+E_{wftd}$

   $F=\frac{(1+\beta^2_1+\beta^2_2)N_{tp}}{(1+\beta^2_1+\beta^2_2)N_{tp}+E_{1st}+\beta^2_{1} E_{2nd}+\beta^2_2 E_{3rd}}$

   
   

   其中 $N_{tp}$ 代表著 True Positive 的數量，$E_{1st},E_{2nd},E_{3rd}$ 是 first type, second type, third type of error。

   其中的小字 $wtudf$ 分別代表著 wrong, true, up, down, flat。舉例來說，$E_{wutd}$ 就代表著 wrong up true down 的數量，也就是預測 up 但實際是 down 的狀況。

   
   

   最後一行就是作者提出的 Weighted F-Score，

   $\beta_1, \beta_2, \beta_3$ 都是屬於可更改的參數，作者分別設定成 $\beta_1=0.5, \beta_2=0.125, \beta_3=0.125$。

   
   

   利用這個 Weighted F-Score 做為指標，是要讓一些情境的懲罰更大，比如預測上漲，但實際下跌時，這樣的損害會比預測上漲但實際是平盤時來得大，調整這樣子的參數，讓模型有比較合理的評估指標。Weighted F-Score 程式碼連結

   
   

   筆者認為該篇論文提出這個評估指標的想法，十分值得參考，畢竟既有的評估指標並不適用於所有任務情境，可以透過不同任務的目標，並提出較適合的評估指標，是一個不錯的想法，甚至未來可以把它改良到 loss function 內，直接讓模型對這個目標做訓練。

實驗結果與結論

作者主要使用自己的模型結構，與其他傳統模型在不同的金融商品中做比較，比較結果如下圖，其中 CDT 1-D CNN 是論文提出來的方法，使用的評估指標是作者提出來的 Weighted F Score，比較有趣的現象是，不使用傳統技術指標時，反而會得到更好的效果。這也是作者在論文中所強調的，使用這個 CDT 1-D CNN 結構可以讓模型去開發出有用的特徵，而這些特徵的算法也與技術指標相似。

（圖片來源：註1）

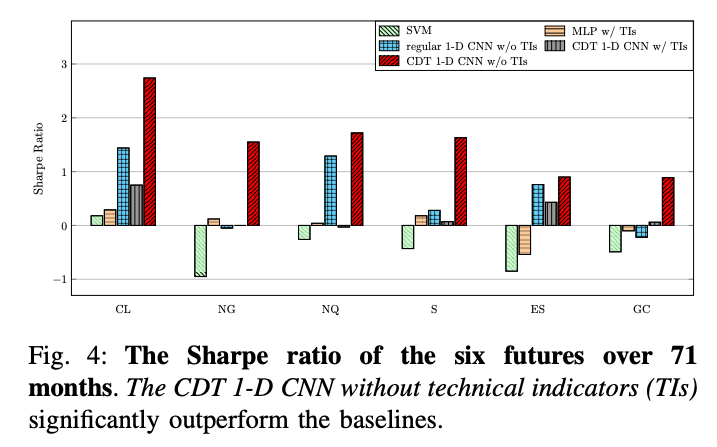
（圖片來源：註1）

在上圖夏普值（Sharpe ratio）的比較上，作者提出來的方法表現得最好。

最後，作者做了一些總結與未來可修改的方向：

1. 可以朝更長的趨勢做學習，當前是兩個小時的資料，未來可以朝向日級別的時間預測。

2. 資料品質，作者覺得在原始資料上有一些遺失，導致在回測方面有出現問題。

1. 標籤的類別，目前是三個類別，漲、跌、平盤，未來可以朝著多類別，如大漲、大跌等多類別的方向做預測。

歸納這篇論文幾個可以學習的方向：

1. 提出一個不需要依賴技術指標的模型結構，CDT 1-D CNN。

2. 定義 y 的方式，參考過去一段時間的變異數，決定下一個時間點的漲幅閾值

3. 提出一個評估指標 Weighted F-Score，在實際交易上會在意的評估指標。

附錄：應用在台指期貨的實驗

* DEMO 程式碼連結

上面的連結是一個小 DEMO，應用在 5 分 k 的台指期貨資料上，有興趣的讀者可以點進去玩玩看，而當中的模型與資料都是用最簡單的方式去呈現。

可以額外去修改的是資料方面可以加入不同的特徵，例如台指籌碼資料、新增技術指標等等的方法增加特徵值。

模型方面後來修改成 transformer 類型的模型會將整體準確率與指標再往上提昇一些，而要注意的是資料上滿容易讓模型 overfitting 在 FLAT 上，所以 DEMO 裡面使用 Class Weight 的方法去改進，當然也能由資料或前處理下手，這部份就留給大家去實驗了，當然除了台指商品之外，其餘的金融商品也可以用類似的手段去讓模型學習，Happy Coding !

• 註1. Financial Markets Prediction with Deep Learning 連結為 https://arxiv.org/abs/2104.05413

• 註2. 回測的設定方法在論文中的第五頁，IV. EXPERIMENTAL SETUP 篇章中的 B-(1) Backtest (From Finance Viewpoint)

（撰稿工程師：王維綱）