在本系列的 [連載之一] 裡，我們已經描述的現代語言學 (不是 1950 年以前那種『傳統』語言學哦！) 是怎麼看待語言的 (一連串性質略有不同，但結構全都一致的函式結構)，而且這個做法也可以解釋，甚至模仿人類的幼童是如何用極少數的資料，就能開始建立他對母語的結構理解。

補充閱讀：[連載之一]  AI 時代的語言學

理解了結構以後，接下來就能計算語意了。

進階單位：語意與 vector

形式語言學裡，研究語意的領域叫做「形式語意學 (Formal Semantics)」或是「邏輯語意學」。一個知識領域一 定要經過「除魅」與「形式化」的個步驟，才真正進入科學的領域。

「除魅」字面意思是「去魔法」，意味著科學方法的出現與開明理性的運用，使世界變得透明、不再有神秘可言。而「形式化」則指的是利用某些數學的方法證明推論的正確性或非正確性。

因此，在語言學裡，雖然有些事情仍是「未知 (unknown)」，但在語言學這個現代基礎學科裡，也是沒有魔法 (magic) 的。

一個最簡單的例子是：

John rented a house in Boston.

它的句法結構可以呈現為^[1]：

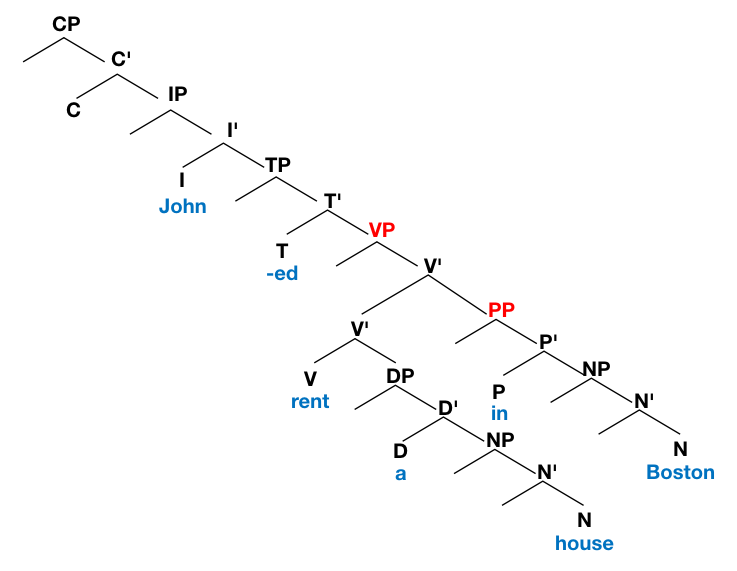
我們就能發現，這句話的語意就是兩件事：

1. John rent a house. (John 租了一間房子)
2. This renting-event happened in Boston. (John 租房子這件事是發生在 Boston)以函式的方式呈現，就可以寫成：
   

內層的 FUNC_rent() 表示的是「租屋」這個函式，而這個函式表達的語意是：

• 被「租」的是 “a house”
• 而發起「租用」這個動作的是 “John”

外層的 FUNC_in() 表示的是「在…(某處)」的函式，這個函式表達的語意是：

• 這起「房屋租用」事件是發生「在」Boston 這個城市裡。

語言學處理 semantics (語意) 時，和詞向量的 vector semantics (向量語意) 最大的不同是「語言學處理的是函式」，而函式本來就可被電腦計算。從「函式」到「語意」之間是一比一的等價關係，函式就是語意，語意就是函式。

那麼「語意的函式」又是什麼意思呢？首先，在卓騰語言科技，我們把 semantics 定義成兩種情況：

1. makes sense: 一段聽得懂，而且也能確定是不是真的語句，表示為 1/1 OR 0/1。我們可以簡單記為 {1, 0}/1
2. not makes sense: 無意義，聽不懂的語句，表示為 1/0 OR 0/0。我們可以簡單記為 {1, 0}/0

當下面這句可理解的句子被看懂的時候：

John rented a house in Boston.

我們究竟知道了什麼呢？我們知道了以下這些事情：

也就是說，語意的計算與事實的核對，具有這樣的語意關係：

相對地，當我們遇到一個讓人聽不懂的句子，像是：「a rent Boston in John house.」 的時候，那麼就是前述的語意關係裡的分母是 0。這麼一來，不論是否真的能在宇宙裡找到 b, j, h，找到的話是 1，找不到的話是 0，但只要分母是 0 ，這個句子的意義就無法被理解。

這麼一來，我們就能明確地定義出什麼叫做「可被理解 (makes sense，分母為 1)」和「不可被理解 (not making sense，分母為 0)」，以及什麼是「事實 (分子為 1)」什麼是「假 (分子為 0)」

相較之下，詞向量的語意和前述的定義無關。它的初衷是因為「字符無法被電腦計算，所以想個辦法把字符變成一組浮點數 (小數)，因為小數可以被電腦計算」。從「詞彙」到「向量」是透過「資料分佈」來做轉換的。而這個轉換不是一比一的等價關係。

一個詞彙會被轉換成什麼樣的向量值，完全是看資料怎麼分佈！

且向量化計算是在「無法處理字符」的前提下，做了一個「假設」。

假設：兩個不一樣的 token X, Y，如果它們的前後 token 的集合「夠相似」的話，那麼 X 和 Y 有相似的語意。

這麼一來，其實我們無法排除「全世界有養企鵝的動物園裡都會出現『token X: 企鵝』和『token Y：餵食工作用的金屬桶』這兩個 token 的週邊環境很相似的可能。」

因此我們會得出「企鵝和金屬桶有某種語意上的相似性」這樣的錯誤結論。

要排除這樣的錯誤結論，只好用更多更多更多更多的資料，讓 token X: 企鵝的週邊充滿了各種其它的東西，好讓 X 和這些『其它東西』的距離相比於 token Y: 金屬桶更近，因此來推出 (腦補出)：『所以企鵝和金屬桶沒那麼相似！』的結論。

這樣做有兩個主要的問題：

1. 最原始的那個 [上下文相似的 X, Y 必然語意也相似] 的假設是沒什麼道理的！

2. 同一個算法既可以得出「企鵝和金屬桶很像」(在資料少時) 和「企鵝和金屬桶不像」(在資料夠多時) 這兩個完全相反的結果。而我們無法預先知道「什麼時候資料才夠多」。更無法排除「當 X, Y 之間的資料夠多的時候，會不會影響 X, K, W, J… 之間的距離(相似度) ？」

因此透過詞向量來計算語意，將會遇上它無法分辨什麼是「可被理解」和「不可被理解」，從以下兩個例子中的 ChatGPT 對話記錄，就能觀察到這點：

ChatGPT 處理「可被理解」的指示詞 (prompts) 時，回覆了正常漢堡的製作流程：

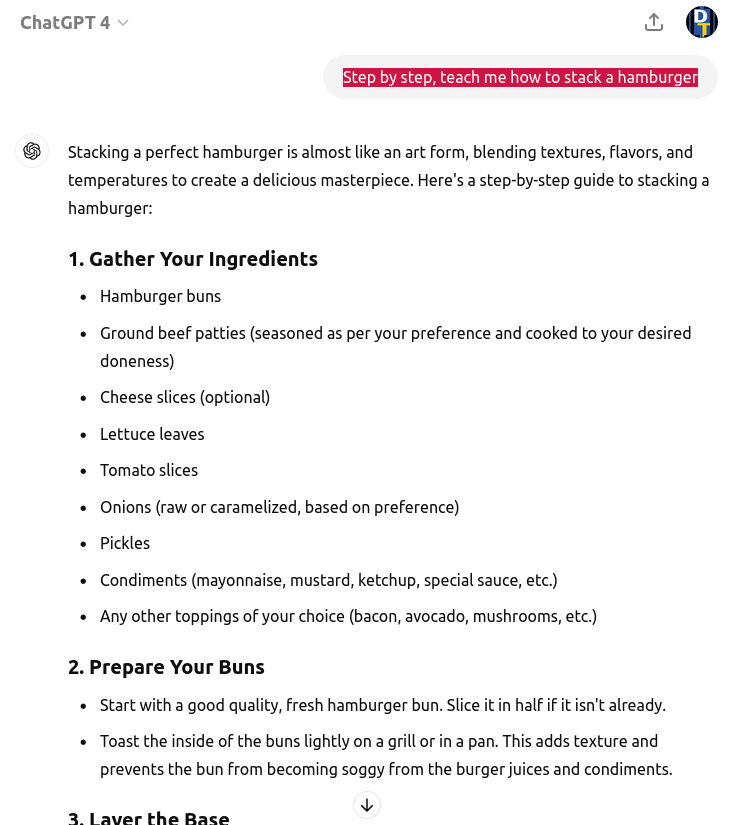
ChatGPT 處理「不可被理解」的指示詞 (prompts) 時，也回覆了正常漢堡的製作流程：

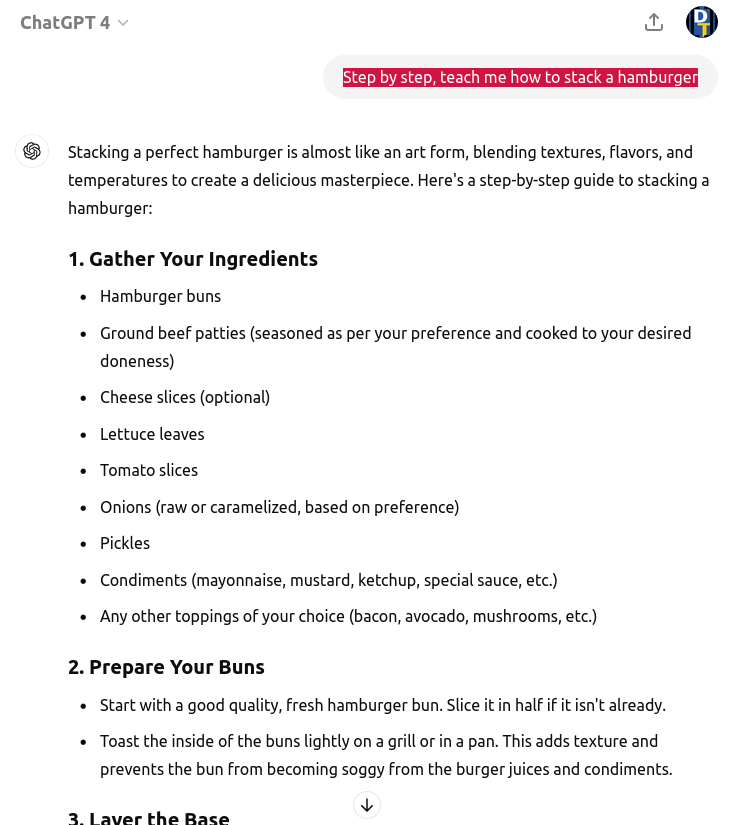
這表示，它其實無法像人類一樣知道「語言的語意是否 makes sense」。

換言之，和人類理解語意的 {1, 0}/1 和 {1, 0}/0 相比，詞向量的語意呈現的是 {1, 0}/{1, 0}。它的分母無法被確定是 0 或是 1，也就是說，利用詞向量做出來的模型並不是真的有辦法計算語意。

更多的例子可以從以下的對比中看出來：

ChatGPT 處理「可被理解」的指示詞 (prompts) 時，回覆了以下的結果：

ChatGPT 處理「不可被理解」的指示詞 (prompts) 時，回覆了以下的結果：

我們可以先忽略它的算式和答案是否正確。那是屬於前述式子裡的分子的「是否能從宇宙中找到符合條件的成員」的事實查核問題。

關於「語意」，我們的重點是放在前述式子裡的分母「能否被正確地覺察語言是可被理解地 makes sense 或不可被理解地 not makes sense」。

很明顯地，任何一個心智正常的中文母語人士都能立刻感覺到，這兩個數學應用問題中的第一個，是可以被理解的，故可以被計算，因此分母為 1，屬於前述的「第一種情況」；而第二個數學應用問題是不可被理解的，故無法被計算，因此分母為 0，屬於前述的「第二種情況」。

但 ChatGPT 顯然無法分辨「什麼是可被計算的，什麼是不可被計算的」，也就是說它分不清楚「什麼是可被理解地 makes sense，而什麼是不可被理解地 not makes sense」。

因此，在 AI 時代裡，語言學的「語意計算」可以更好地和生成式大型語言模型做搭配，將「無法被理解」的語句加以標出、排除或是拒絕處理，以便讓本質為接龍模型的 LLM 可以產出品質更好的結果。

而我們從語言學的角度出發，可以這麼做，是因為我們知道語言具有內部結構 (如系列文一所述)，而且這個結構可以被描述為一個可被計算與繼承的程式函式。

在本文中，我們進一步延續這個概念，將結構內的每個詞彙，依其在句法結點上的位置，直接轉寫為一組函數關係。並據以解釋「什麼是具有 comprehensibility (可被理解性)」的句子，說明「makes sense vs. not makes sense」的差異。也說明在一個 makes sense 的語意前提下，什麼是「真實」什麼是「虛假」的計算。

在下一篇系列文中，我們將進一步展示，利用這樣的語意計算能力，我們可以做哪些應用。

本文取得《卓騰語言科技 - 科普分享空間》授權轉載，原文詳見AI 時代的語言學 - 連載之二：結構