想提高模型準確性？試試利用CO-SNE降低階層結構資料的維度

在數據分析時，有一種資料類型是資料間具有階層結構（hierarchical-structure data），例如社交網路、RNA結構等，後續能應用在推薦系統、結構預測等議題上。這類資料通常希望可以在分析時，盡量保持原始的資料結構關係。如果讓很多維度的資料在降維後，仍然保持資料結構的關係，無疑可以大大提高模型預測的準確性。以下是UC Berkeley的Guo等人在2022年6月提出的新方法。

高維度資料集的挑戰

現實資料中有許多由大量特徵組成的高維度資料集，這對資料處理、訓練模型、視覺化、結果解釋等往往造成巨大困擾。常用的方法是先將資料集的多特徵，「降維」成較少的特徵以便後續處理。我們通常會先將資料以歐式空間（Euclidean space）表示，常見的降維技術降維包含：Principal Component Analysis (PCA)、T-distributed Stochastic Neighbor Embedding (t-SNE)、Uniform Manifold Approximation and Projection (UMAP)等。

然而，許多領域的資料是階層結構型資料（hierarchical-structure data），如社交網絡、演化樹、蛋白質結構等，這種類型的資料若是利用歐式空間（Euclidean space）表示，會造成結構訊息的變形，因此常利用雙曲線空間（hyperbolic space）表示，能夠近似該資料類型。其常用的降維方式是先利用如Poincaré ball model獲得各資料在雙曲線空間的表徵位置，然後再進一步透過如UMAP、PCA via Horospherical projection （HoroPCA）等方法進行降維。

由UC Berkeley的Guo等人[1]在2022年六月發表於Conference on Computer Vision and Pattern Recognition的新方法：CO-SNE，主要就是針對階層結構資料進行降維。

CO-SNE 介紹

CO-SNE的設計是基於t-SNE進一步進行改良，接下來筆者將說明t-SNE與CO-SNE的異同。兩者相似的地方都是，「使低維度空間的資料點距離分佈與高維度空間的資料點距離分佈相似，以期降維後保留資料之間的關係。」基於這樣的概念，CO-SNE首先將t-SNE從歐式空間表徵改成雙曲線空間進行表徵，使其能更好地表示階層結構資料。

不同於t-SNE將高維度空間的資料點距離，以常態分布對應到低維度的Student’s t分布；CO-SNE將高維度的資料點距離，以常態分佈對應到低維度柯西分布（Cauchy distribution）[表一]。

表一：t-SNE與CO-SNE假設之空間距離分布的比較

	t-SNE	CO-SNE
高維度空間的距離分布	Euclidean normal distribution	Hyperbolic (Riemannian) normal distribution
低維度空間的距離分布	Euclidean Student’s t-distribution	Hyperbolic Cauchy distribution

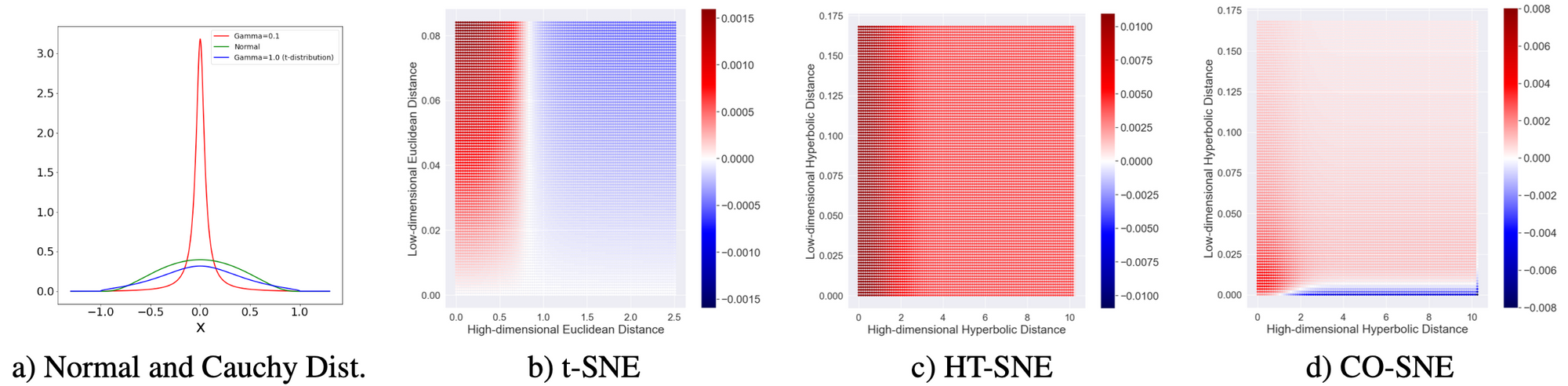
CO-SNE之所以不將高維度的資料點距離以常態分佈對應到低維度的Student’s t分布，是因為在雙曲線空間當中，常態分佈和Student’s t分布在兩側尾端差異不大，甚至常態分布略高 [圖一(a)]。因而不能在高維度空間下，達到當「距離越遠（兩側尾端）的兩個資料點，降維後也傾向距離越遠」的目的。而CO-SNE之所以改採用柯西分布作為低維度的對應分布，主要是採用了另一個策略角度，也就是期望「高維空間越近的資料點投影到低維度時也越近」。我們可以在圖一(a)中看到柯西分布在距離零的時候有最高的機率。

圖一：雙曲線空間的距離分布與維度轉換對應的梯度[1]。
a)雙曲線空間的距離機率分布（x軸：高維度空間標準化距離；y軸轉換到低維度空間距離的機率密度）。綠色：常態分布；藍色：Student’s t 分布（𝛾=1.0）；紅色：柯西分布（𝛾=0.1）。
b) 歐式空間中的t-SNE梯度熱圖。
c) 雙曲線空間中的t-SNE熱圖。
d)雙曲線空間中的CO-SNE熱圖。

從另一個角度驗證這個設計的好壞，也就是將資料點在高維度的距離當作X軸，以對應到低維度的距離當作Y軸，畫出梯度熱圖進行觀察。梯度越低，表示資料點對應到低維度時排斥性越大、越容易分散，相反地梯度越高，表示資料點對應到低維度時吸引力越大、越容易聚集。透過比較低維度時距離相近的狀況（y: 0.000~0.025），可以觀察到雙曲線空間中的t-SNE [圖一(c)] 在高維度空間的距離越遠，對應到低維度的時候並不會分散，而CO-SNE [圖一(d)]卻能夠分散，符合目標。

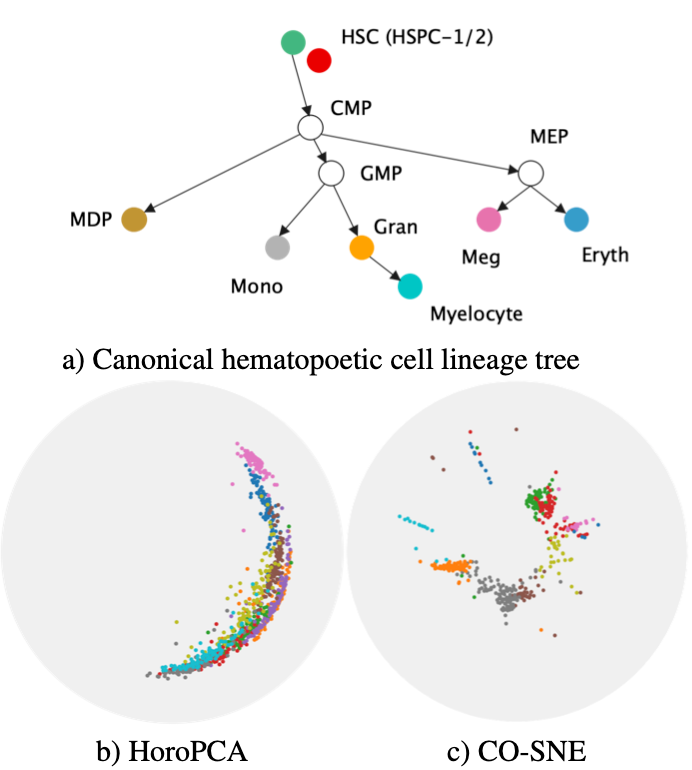
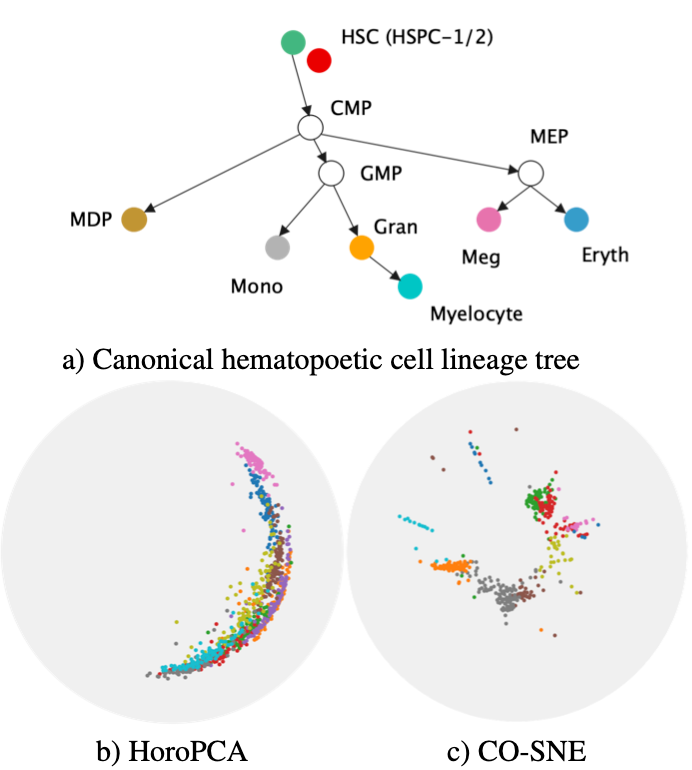
以上是CO-SNE的設計思路，接著讓我們看一下CO-SNE的視覺化效果吧！比較一下專門為雙曲線空間設計的HoroPCA、CO-SNE兩種降維技術，我們可以從圖二觀察到CO-SNE降維後可以保留較好的全局結構性以及局部相似度。